By

文章目录
  1. 1. Perceptron
  2. 2. Perceptron Learning Algorithm (PLA)
  3. 3. PLA 算法是否能正常终止
    1. 3.1. wf和wt越来越接近
    2. 3.2. wt会缓慢的增长
    3. 3.3. 证明收敛
  4. 4. 线性不可分的PLA
  5. 5. 参考

Perceptron

先来看一下一个经典的信用卡发放问题：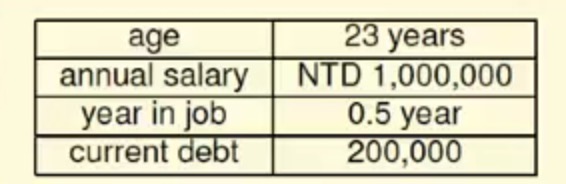

这是一个用户的基本的信息，现在要决定是否对他发放信用卡。

现在假设这些基本信息组成了一个向量X={x1,x2,…xd}
同时对于每一维度上有一个对应的权重向量W={w1,w2,…wd}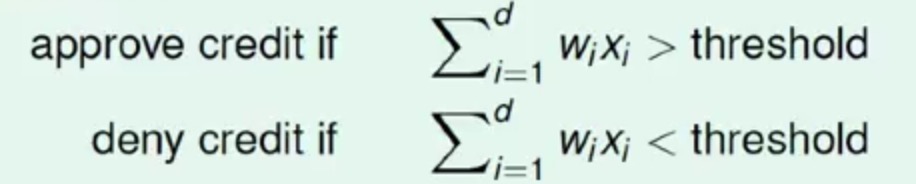

那么如果这两个向量乘积出来的值大于一个设定的阈值，我们就发他信用卡，否则就不发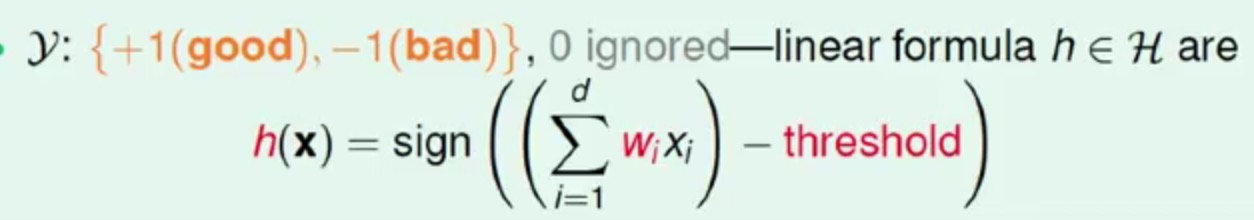


相应的表示：

  • y=+1 表示发卡，y=-1表示不发
  • sign是一个取符号函数sign(x) = 1 if x>0, -1 otherwise
  • 这里的h与wi的权重有关，以及与阈值threshold有关，这里的h就是叫做感知机
有了以上描述之后，我们需要电脑做的就是通过个人的基本信息以及每个维度上的权重算出一个分数值，如果这个分数值大于一个设定的阈值，如果超过这个阈值，最终得到的就判定给该用户发卡，否则不发信用卡。

这里我们将阈值threshold做一个简化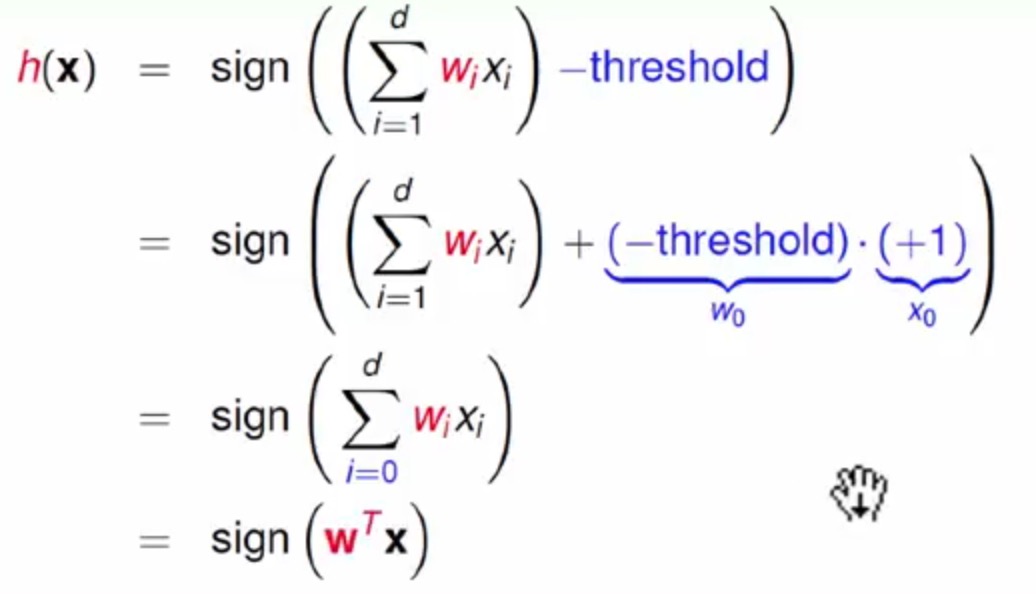

相当于是加一个第0维度，该维度上的权重就是这个阈值，这么做的好处就是h就变成了两个向量的内积

好，用形象的方式来表述，下面当只有2个属性的时候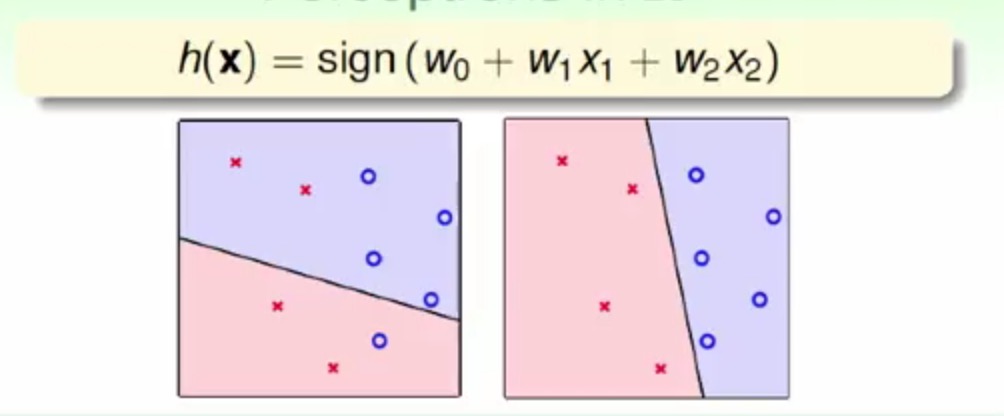

  • (x1,x2)可以构成平面上的点
  • 标签值y：圆圈表示+1,叉叉表示-1
  • h就表示为平面上的线，其中线的一端是+1，另一端是-1

所以，感知机其实是一个线性的二元分类器

还有，该平面上其实有无线条线（也就是hypothesis set），那如何能找到一条最合理的线(hypothesis)来完成发放信用卡得判断呢？

Perceptron Learning Algorithm (PLA)

现在我们是需要找到一个g(x) 这个g(x)≈f(x) 最近越好，也就是yn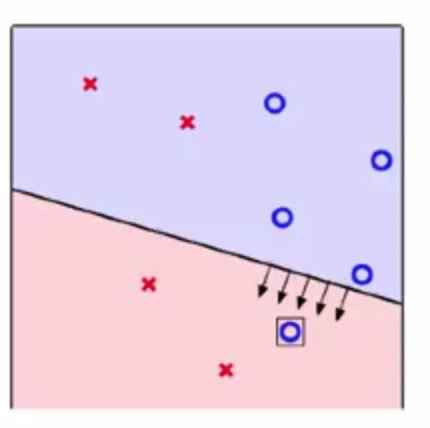

首先我们从一个随机的线g0出发，这个g0可能不够好(这个g0这根线可以使用w0这个向量来表示，初始时都是0向量)，所以我们需要调整w的值来判断的改进学习g(x),直到到每个gn的时候每个点都判断正确(这里的t表示当前的一个样本点)


那么如果这个线还不够好的话，那么必定存在一个点，它是分类错误的(犯错)，我们现在就可以根据这个点来进行调整
那么就会有两种情况：

  1. 我要的是yn=+1，但是经过g(x)之后为-1，那么也就是说w和x向量的角度太大，我们需要转向x端，也就是更新为w:=w+x
  2. 我要的是yn=-1，但是经过g(x)之后为+1，那么也就是说w和x向量的角度太小，我们需要远离x端，也就是更新为w:=w-x

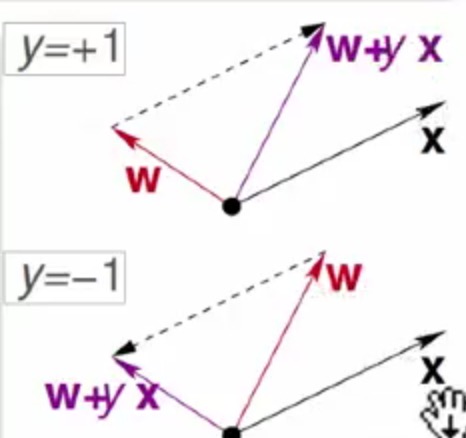
    最终用一个式子来表示w的更新就是为

    直到这根线不再犯错，那么整个过程就是叫做Perceptron Learning Algorithm (PLA)

那如果简单的判断当前的线g有没有犯错误？一种常见的方式就是使用cycle PLA

这整个过程描述如下：

  1. 假设现在有n个点，我们从1,2,3到逐个遍历过去
  2. 如果当前的点没有犯错，那么我们进入下一个，否则我们就做刚刚的错误修正，然后再进入下一个点
  3. 直到遍历了n个点又绕回来并且全部没有错得时候停止

这里的循环时可以依次1~N进行遍历循环，也可以进行乱序循环(建议^_^)

现在留下两个问题：

  1. PLA在学习过程中一定会停下来吗？？
  2. 最终学习出来的先g能适用于训练以外的样本吗？

PLA 算法是否能正常终止

先来看一下下面的几种数据情况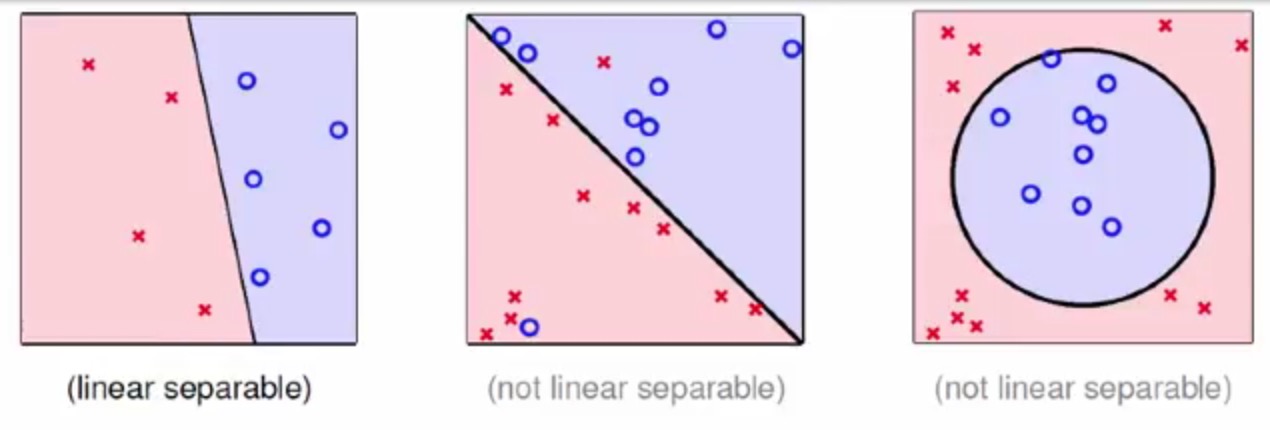

其中第一幅图为线性可分，第二、三幅图为线性不可分

其中PLA算法只能在线性可分的数据下才可能终止运算（因为在线性不可分的数据中铁定没有那么一条线来划分两类数据，连线都没有，谈何停止）
现在假设有存在正确分类的线wf,wt为训练时的线

wf和wt越来越接近

  • 那么该线与任意一点的内积乘以标签值一定是大于0的，也就是说其最小值是大于0的（上图的蓝色部分）
  • 同时在学习训练过程中，在进行w全职的矫正之后，矫正点与当前权重的内积与目标值的乘积一定是大于目标权重相应计算值的最小值的(红色部分)

现在来看一下目标权重wf与当前训练权重wt的关系（两个向量的内积可以衡量他们的相似度,表示角度上的接近）

从上面的式子可以看出，每作出一次矫正，目标权重与当前权重的相似度就更加进一步，也就是说明每一次矫正权重是有效的

wt会缓慢的增长

因为PLA算法在只有犯错（预测错误）的时候才会进行权重的矫正，那么犯错的判断为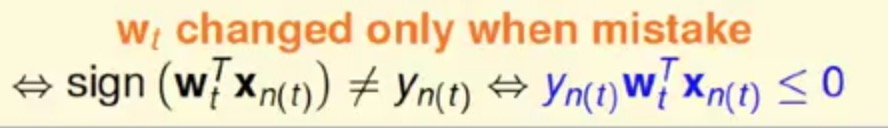

现在来看wt矫正（增长）之后的值wt+1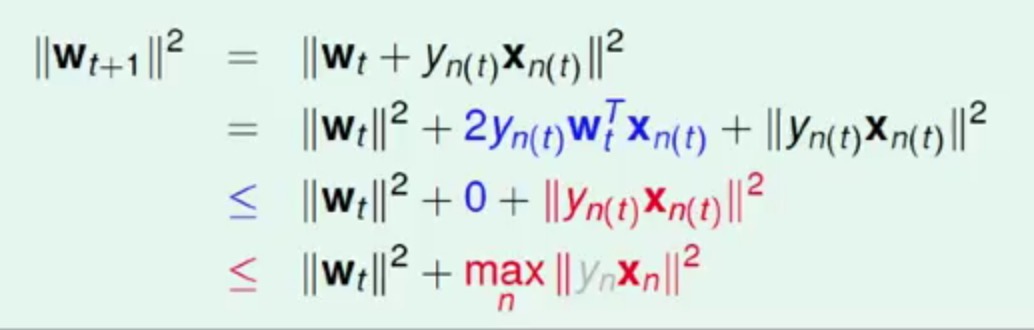

其中蓝色的部分正好为判断错误的不等式，恒小于0，而红色部分使用最大的点来代替之后，不等式成立
所以增长时wt+1由上一个xn决定，并且是在一个有界的范围内增长，比较缓慢。

证明收敛

结合以上两个式子，可以得出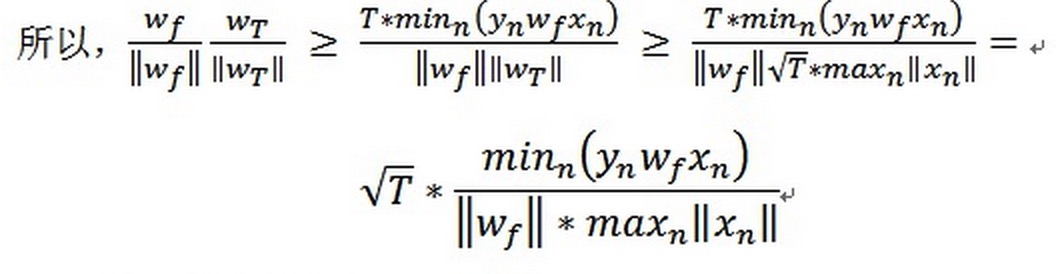

这表示两个正规化向量内积，为他们真正的相似
其中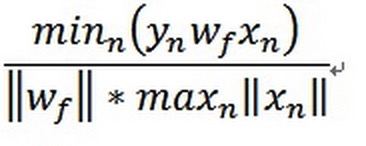
为一个常数
所以可以得到随着T的越来越大，wf,wt的夹角会越来越小，
向量夹角余弦值不会大于1，可知T 的值有，证明了简单的PLA 算法可以收敛，也就是他会停下来 。

在

  1. 数据是线性可分的，wt会越来越接近wf
  2. 总是在犯错的情况下进行权值的矫正，wt会进行一个缓慢的增长
    的条件下，最终简单PLA会正常终止

线性不可分的PLA

如果得到数据是线性不可分怎么办（数据里面还有噪声），此时简单的PLA无法收敛

但是我们有一种退而求其次的方法

在学习PLA算法的时候最终不一定要每个点都进行正确地划分，而是求最终出来的线分错的点最少（这根线不是完美的线，但是是一个最优的线）
但是求解那个最优的线是一个NP难题-_-

下面来介绍一种叫Pocket Algorithm算法可以近似的求解最优

该算法与简单PLA最大的区别就是：

  1. 它不是一轮一轮的遍历数据，而是去随机取一个点来进行判断
  2. 只有当矫正了权重之后的犯错率（见那个min的公式）小于当前的权重的犯错率时，才会进行权重的更新

    这里的检测错误率额代价很大，应该是要遍历一遍样本才可以知道-_-

  3. 它是提前设定了迭代次数

参考

配图均来自《台湾国立大学-机器学习基石》

本作品采用[知识共享署名-非商业性使用-相同方式共享 2.5]中国大陆许可协议进行许可，我的博客欢迎复制共享，但在同时，希望保留我的署名权kubiCode，并且，不得用于商业用途。如您有任何疑问或者授权方面的协商，请给我留言。

文章目录
  1. 1. Perceptron
  2. 2. Perceptron Learning Algorithm (PLA)
  3. 3. PLA 算法是否能正常终止
    1. 3.1. wf和wt越来越接近
    2. 3.2. wt会缓慢的增长
    3. 3.3. 证明收敛
  4. 4. 线性不可分的PLA
  5. 5. 参考